Preliminary Results of TrueGrid’s Automatic Quadrilateral Shell Mesh Generator

By DE Editors

September 2, 2010 - XYZ Scientific Applications, Inc. is planning to release an automatic structured all quadrilateral shell mesh generation feature called AutoQuad late in 2010. Of course there are many products on the market that offer automatic shell mesh generation. But the new TrueGrid AutoQuad has some unique features that make building a high quality all quadrilateral mesh easy. In particular, the projection method is used so that the quality of the mesh is not influenced by the way the geometry is rather arbitrarily split up by the CAD or solids modeler. This is explained below. Also, AutoQuad produces block structured meshes with the minimum number of irregular node while maintaining mesh on the boundary. This is also explained below in greater detail.

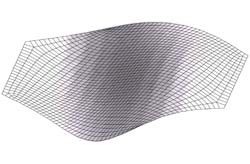
A single surface is used in the example below. It has some curvature, but it was kept at a minimum to make it easier to view the resulting surface mesh.

The process of building the all quadrilateral mesh is quite simple. Select the AutoQuad mesh option, which activates the popup window shown in the picture. Then select the surface using the mouse in the picture. The surface can be a simple or a TrueGrid composite surface.

The next step is to select the nodal distribution along the boundary of the surface. This can be as easy as choosing the number of nodes or the size of the edges between nodes. There is a rich selection of additional options for boundary selection and nodal distribution. The boundary nodes for this example were selected automatically and require no input. from the user.

A new technique has been developed for the TrueGrid AutoQuad feature that chooses the best multi block topology based on the shape of the boundary of the region to be meshed. The best topology is the one that has the fewest number of irregular interior nodes. A regular interior node is one that is connected to 4 quadrilaterals. An irregular node is one that is connected to 3 quadrilaterals or it is one that is connected to more than 4 quadrilaterals. Irregular nodes can be the source of some of the greatest numerical errors in a simulation and by keeping the number of these type of nodes to a minimum, one can reduce the numerical errors in the simulation. However, in most cases, it is impossible to eliminate all irregular nodes without producing a bad mesh at the boundary, so some irregular nodes should be expected for all but the simplest of mesh problems.

In this example, there are 20 nodes along the left boundary, 19 nodes along the right boundary, 54 nodes along the top boundary, and 57 nodes along the bottom boundary. It is not possible to place a single block mesh with this boundary selection. For this reason, there are 8 irregular nodes in the resulting mesh. In the future, there will be an improvement for this case. There are several options that could be used. For example, a transition region on the left boundary can be used to even out the remainder of the boundary nodes so that the rest of the surface can be meshed using a block mesh with 53 by 19 nodes. This has 5 irregular nodes, but they are concentrated at a corner of the surface.

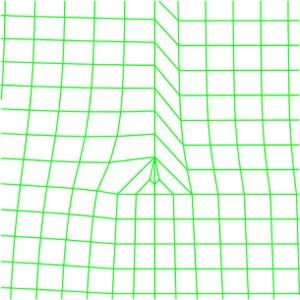Alternatively, the transition region could be placed at the center of the mesh, as shown in the picture. This also has 5 irregular nodes, but they are placed away from the boundary where the highest stresses are likely to be. This is probably better. Further research is needed to determine if this is the optimum topology for this type of problem.