Beyond Quality Control

By K.N. Amarnath

Product quality in any arena can be traced back to variations in parts, materials,people, and processes. And since it has been observed that all work can be brokendown into processes, all processes, manufacturing or administrative in nature,have inherent variability. That variability has a directly proportional effecton process quality: The larger the variations, the poorer the quality.

Systat’s DOE Wizard provides an alternative interface consisting of a seriesof questions defining the structure of a design.

Basic statistical process control techniques such as Pareto analysis, cause andeffect diagrams, and control charts have been successfully incorporated in manyindustries. And while these tools are useful in identifying variations and inkeeping the process quality from deteriorating, they do little to dramaticallyimprove quality of the end product, and are used primarily for maintenance andmonitoring purposes.

To make those improvements, experiments must be completed to determine how asystem responds to a change in some factors. These types of experiments are undertakento optimize the system’s performance, or to characterize the system as part ofa validation effort. Careful planning at the outset of such experiments can savea great deal of time and effort.

If the system response depends on just one factor, the strategy is simple: Measurethe response at several different values of the factor and fit a curve to theresults. But when there is more than one factor, things become more complicated.

The traditional approach would be to vary each factor individually while holdingthe others constant. This approach does work (i.e., one gets an idea how the systemresponds to changes in the factors), but it is not the most efficient way to goabout the investigation. When investigating a process, you often have to considermany factors that may influence the process. The simple approach of testing onefactor at a time can lead to problems due to interactions.

For example, the effect of temperature on a chemical process may be very differentat low pressure than at high pressure. If you did two simple experiments, oneexamining temperature and one examining pressure, you would never see the effectsof temperature changes at different pressures.

A more accurate way to study the effects of changes on a system is through designof experiments (DOE), or statistical experimental design. DOE, a planned approachfor determining cause-and-effect relationships, can be applied to any processwith measurable inputs and outputs. Factorial designs enable evaluation of multiplefactors simultaneously. A factorial design for the example above could includeobservations at four points: high temperature/high pressure, high temperature/lowpressure, low temperature/high pressure, and low temperature/low pressure. Thishelps you see the effects of different temperatures at different pressures.

DOE provides a statistical means for analyzing how numerous variables interactand has been applied to improving quality in numerous types of systems since SirRonald Aylmer Fisher applied it to agricultural experimentation early in the 20thCentury. Since then DOE has spread to numerous fields and has found wide acceptancein engineering.

Systat DOE generates design matrices for a variety of analysis of variance. Youcan use Systat DOE as both an online library and a search engine for experimentaldesigns, saving any design to a Systat file. You can run the associated experiment,add the values of a dependent variable to the same file, and analyze the experimentaldata by using a General Linear Model (or another Systat statistical procedure).Systat offers Classic DOE, the DOE Wizard, and the Design command for generatingexperimental designs.

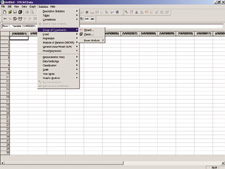The Systat Design command interface.

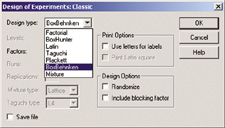
Different kinds of factorial designs can be generated in Systat, including homogeneousfractional, mixed-level fractional, Box-Hunter, Placzkett-Burman, Taguchi, andLatin square designs.

In many industrial situations, you need to find the best combination of factorsfor your process, as measured by some response variable. In such instances, responsesurface methods can help you find the optimal conditions for your process. Thebasic approach is to take measurements at different levels of each factor andthen to build a model of the response in terms of those factors. The model isexpressed as a polynomial approximation.

The process of fitting a response surface is usually an iterative one, usinga hill-climbing strategy. You start with some set of factor values (chosen becausethey are thought to be close to the optimum or because they are convenient), andyou conduct an experiment to find a linear model, a model with only main effects.(Two-level factorial designs are useful for this stage of the process.) If thelinear model fits, it is used to find the direction of steepest ascent (or descentfor minimization problems), and the factor levels are adjusted in this directionto bring them closer to the optimum. This is repeated until you find that a linearmodel does not fit the data and that a quadratic model, a model that includesinteraction terms and squared main effects, is required. Then a final experimentis conducted to estimate the quadratic model and identify the optimum values.(While the quadratic surface may not fit the global response function very well,it usually fits quite well for localized regions of the factor space.)

Two general response surface designs are available in Systat, namely, CentralComposite and Box-Behnken designs. Apart from all the others previously mentioned,Systat also provides mixture designs and optimal designs. The former takes intoaccount this interdependence of factors by assuming that the factors must havea sum equal to a constant value. The latter minimizes a variance criterion (theobjective function) within the constraints of the experiment that include thefollowing methods: Fedorov, k-exchange, and coordinate exchange algorithms. Thereare three optimality criteria available for Fedorov and k-exchange algorithms,and two available for coordinate exchange algorithms.

DOE’s potential for application in industry includes, but is not limited to,reduced time in product and process design and development; reducing the effectof variations in manufacturing conditions; improving process performance; increasingprocess productivity by reducing scrap or rework; and making products robust towithstand environmental variations. It is a very powerful problem-solving techniquethat assists engineers in tackling quality control problems effectively and economically;independent research has shown that DOE can help to improve a company’s positionin the marketplace, from securing a competitive advantage to increasing profitmargins.

Quality Improvement for Robust Design
A large measure of the popularity of design of experiments (DOE) methodologyin industry can be traced back to the quality engineering methods of Dr. GenichiTaguchi, who was recruited to help correct postwar Japan’s crippled telephonesystem. In the 1950s he developed his own methods for identifying design problems,and were it not for the advancements Taguchi made, Japan might not have stayedafloat after World War II let alone flourish.
   Japanese manufacturers were struggling to survive with very limited resources,and Taguchi revolutionized the manufacturing process in Japan through cost savings.He understood, like many other engineers, that all manufacturing processes areaffected by outside influences, or noise. However, Taguchi realized methods ofidentifying noise sources with the greatest effects on product variability. Hisideas have been adopted by successful manufacturers around the globe because oftheir results in creating superior production processes at much lower costs. Heis widely acknowledged as a leader in the U.S. industrial quality movement, andis credited for starting the Robust Design movement.    K.N.A.

K.N. Amarnath is a Product Analyst with Systat Software. He has more than 10 years of experiencein synthesis, modeling, and analyzing data. His research interests include interdependentmultivariate data analytical methods and data mining techniques. Contact him viae-mail c/o Desktop Engineering Feedback.