Novel Machine-Learning Methodology Refines Simulation of Heart Anatomy and Function
Rapid optimization technique for mitral-valve modeling is applicable to other cardiac structures.

FE model of a closed mitral valve (green) and the chordae ligaments (yellow) that attach the valve leaflets to the papillary muscles. Image courtesy of Thornton Tomasetti Applied Science.
Latest in Finite Element Analysis FEA
Finite Element Analysis FEA Resources


Dassault Systemes

Latest News
November 21, 2018
By Reza Salari, Thornton Tomasetti Applied Science
Finite element analysis (FEA) is a fundamental tool underlying simulation-guided product development in life sciences, allowing the evaluation and prediction of the behavior of implanted medical devices and their interactions with human tissues. Great strides are being made in the industry, yet the individuality of every human being creates a moving target for clinical and commercial success. Going from accurate modeling of normal organ and tissue behavior to patient- and/or disease-specific simulations remains a significant challenge.
When evaluating heart disease with simulation, one approach to creating diseased-state models is to generate 3D models and FEA meshes from patient-specific imaging data such as CT scans and/or MRI. While the associated segmentation software has improved significantly, this process can still be extremely time-consuming. Very importantly, it also may not capture all the details required for the simulated behavior to match the true diseased state, especially when there is motion involved—as is obviously the case with a beating heart.
An alternative approach, one that can even be used in conjunction with scan-based segmentation methods, is to modify a pre-existing, reasonably representative, FEA model in a way that allows the simulated behavior of the heart to match the targeted behavior seen in the diseased state. Our group has developed a shape-matching, inverse finite element framework that can be applied to develop simulations of the mitral valve (MV) that are a closer fit to the behavior seen in diseased states. This has the potential to be applicable to modeling patient-specific organ behavior going forward. We presented this work to the ASME 2018 V&V (Verification & Validation) Symposium.
In the case described here, we started with the Living Heart Human Model (LHHM, from Dassault Systèmes), which provides a baseline FEA model that fairly accurately represents a beating, healthy heart. (Our methodology can be applied to 3D heart models developed from other sources as well.) From the LHHM we created a submodel of the mitral-valve region alone—consisting of the mitral annulus, leaflets, and chordae—for greater efficiency. Not surprisingly, the submodel ran in less time than a full heart simulation, though with the same fidelity. Then, to improve run time even further, we developed a proprietary technique that creates a surrogate model from the submodel, harnessing machine learning to optimize results in a matter of minutes instead of the hours that a submodel might take to run.
Here’s how we developed this novel methodology.
Setting up the Mitral-Valve Submodel
Located between the left atrium and the left ventricle of the heart, the mitral valve (MV) is made up of two leaflets that contract tightly together with each beat, briefly sealing off the ventricle so it can push oxygenated blood to the rest of the body. When a myocardial infarction (heart attack) occurs, heart-muscle tissue death can negatively affect the function of the chordae tendineae—the many slender ligaments that attach the leaflets to that muscle.
Malfunction of the chordae results in incomplete coaptation (closure) of the leaflets and leakage of blood back into the atrium. This results in the disease state known as mitral-valve regurgitation; the patient receives less oxygen than normal and becomes out-of-breath and fatigued. Patient-specific computer simulations of this condition can aid clinicians in educating patients, enable surgeons to customize interventions, and help researchers develop new corrective strategies.
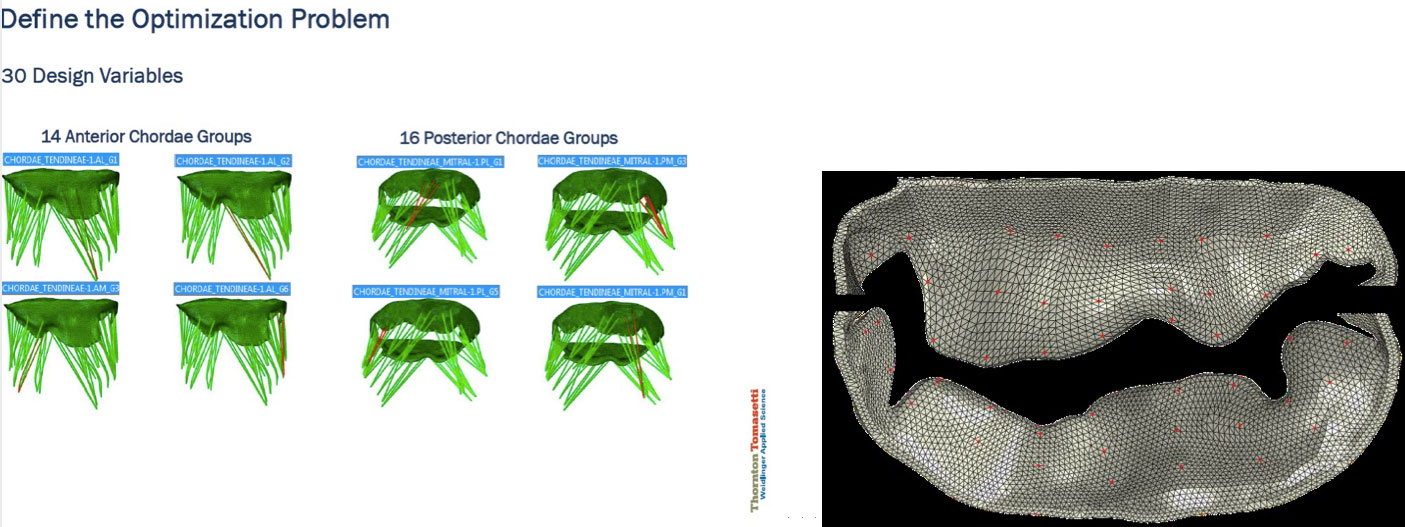
To create a diseased-state mitral-valve model, we started with a baseline FEA submodel of a healthy mitral valve taken from the LHHM, which includes all the relevant parameters needed to simulate MV behavior: meshed geometry of the mitral annulus and leaflets (both shape and thickness), mitral-leaflet material properties and fiber orientations, the number and placement of the chordae, chordae material properties, length and connection to the leaflet (“zone of influence”) and the properties of the associated papillary muscles.
This baseline model does not exist in isolation: its motion is driven from global (full) heart-model boundary conditions, as are the pressures on the bottom surfaces of the mitral leaflets that reflect the pressure difference between the heart’s left atrium and ventricle. But of course considerable run time is saved with this smaller model when compared with conducting the valve analysis inside a full-heart model.
Inverse FEA Solution
Some parameters that most acutely affect the behavior of the mitral-valve submodel include leaflet geometry and material properties, chordae length, thickness and material properties, chordae connection to mitral leaflets, etc. Given a diseased-state mitral-valve shape, the question is what adjustments to these submodel parameters are needed in order to most closely represent the behavior of the diseased valve.
To answer this question, where the model output is already known and you are looking to identify what input to your model caused the known output, we turned to an inverse finite-element approach. We adjusted the parameters and updated the submodel in an iterative and systematic way. At each iteration we compared the results of the updated submodel against the target state with the goal of minimizing their differences through an optimization process. Iterations continued until the tuned submodel represented the diseased shape with the desired accuracy.
To keep the model size down, we focused on adjusting the chordae lengths—although the problem can be extended to include other influential parameters mentioned earlier. We leveraged Isight process automation and optimization software to build the inverse finite-element framework. The mismatch between the target and the simulated leaflet shapes was measured through a function that described the difference between the simulated and target positions of a finite number of preselected matching points. The mismatch was minimized through subsequent model iterations by updating the length of the chordae. As the discrepancies were reduced, a closer and closer approximation of the actual disease state was achieved.

Reducing Runtime from Hours to Minutes with a Novel Algorithm
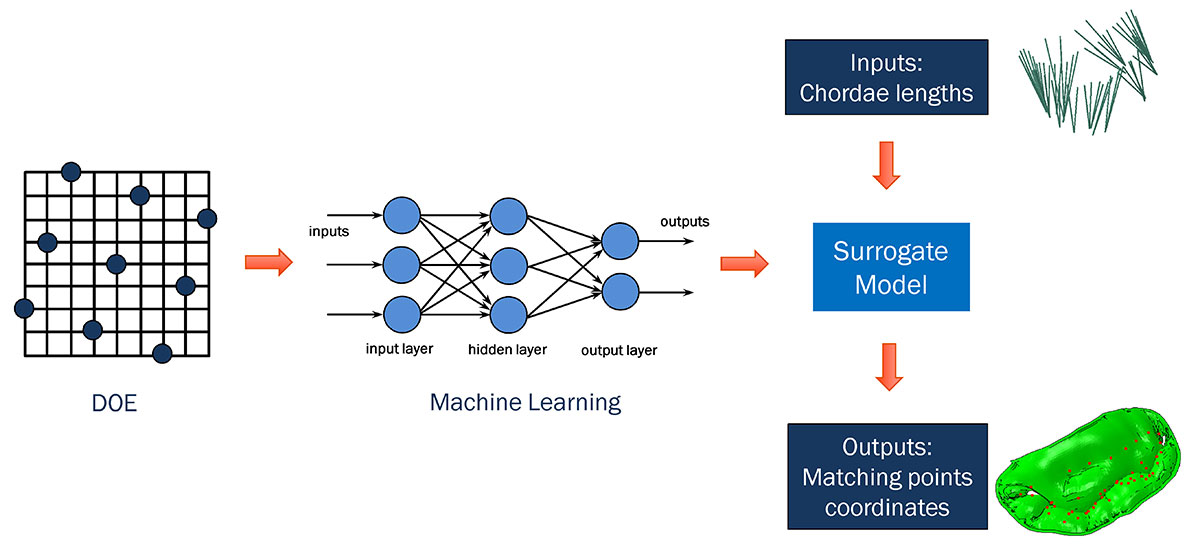
This mitral-valve submodel analysis, although quite accurate, was also the most time-consuming part of our methodology, taking nearly half an hour per iteration to run—with hundreds of iterations needed to reach the best match of leaflet shape to disease state. For greater efficiency, we decided to investigate how machine learning might be used to substitute a faster-running surrogate model for our high-fidelity submodel.
Starting from a design of experiments (DOE) setup of our mitral-valve simulation problem, we used machine learning in conjunction with a proprietary algorithm to effectively generate the same submodel output (describing leaflet position) in far less time. The algorithm removed the necessity of re-running the submodel every time there was a change in chordae input, and provided similar results to those from the submodel with minimal loss of accuracy.
The surrogate model was then dropped into an Isight optimization loop, which ran much more quickly than before. This allowed us to go from initial shape to target shape in just a few minutes, rather than many hours.
A Widening Field of Applications
We initially developed this new methodology for mitral-valve modeling, and are now applying our process to the tricuspid valve as well.
We are also working to make this kind of time-saving analysis available for other structures, such as the blood vessels around the heart. Starting with CT scans of arteries, we are using our proprietary algorithm to fine-tune blood-vessel models to optimally match artery shapes during heart contraction and relaxation.
More Dassault Systemes Coverage

For More Info
Reza Salari has two decades of experience in computational mechanics. His work is mainly focused on the development and use of finite element analysis-based methods to solve challenging problems in a variety of industries, ranging from life sciences to structural engineering. He is an Associate at Thornton Tomosetti.
Thornton Tomasetti optimizes the design and performance of structures, materials and systems for projects of every size and level of complexity. An employee-owned organization of engineers, scientists, architects and other professionals collaborating from offices worldwide, we support clients by drawing on the diverse expertise of our integrated practices.
Subscribe to our FREE magazine, FREE email newsletters or both!
Latest News